真的全忘了。。。 #泊松、指数、伽马分布

• 泊松分布： 已知某事件单位时间的平均发生率$\lambda$，能给出单位时间内实际上发生X次的概率。可以证明二项分布取极限（试无数次）就是泊松分布，也就是说二项分布是泊松分布在离散的时间上的对应。
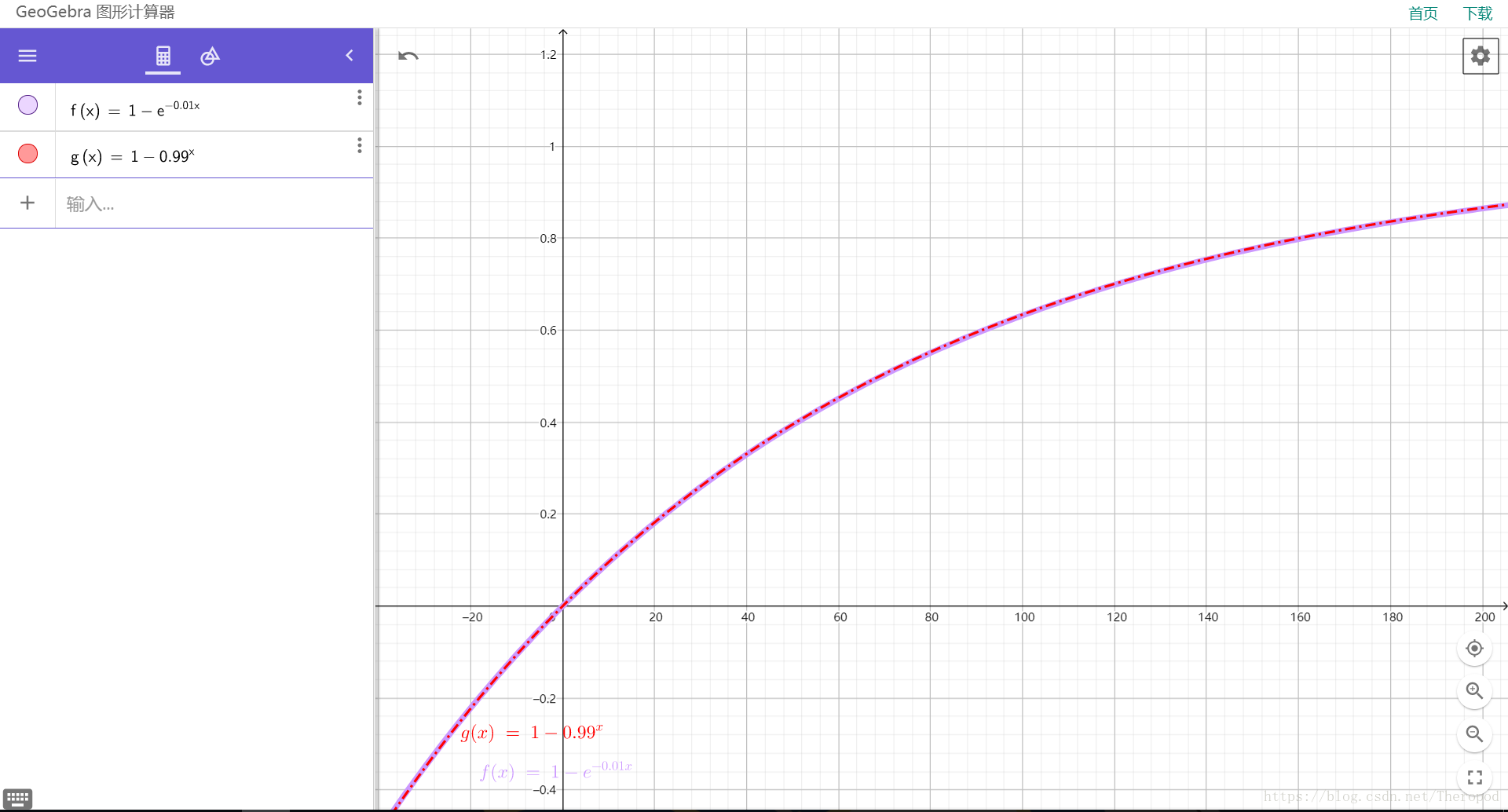
• 指数分布： 泊松过程中，第k次随机事件与第k+1次随机事件出现的时间间隔t服从指数分布，即 $t\sim Expotional(\lambda)$ 。可以发现指数分布的累积分布函数（注意不是概率密度函数）：$1-e^{-\lambda t}$ 中的$e^{-\lambda t}$ 就是泊松分布中t个时间内不发生事件的概率。 这个累积分布函数只是说出现，而不管出现几次，其实和直接用二项分布计算（1减去每次都不出现的概率）基本上相同，只是一个用概率的乘方，一个用$e$来表示。比如说计算0.01概率出5星的抽卡，可以用下面的两种式子计算，而得到的函数曲线基本上是重合的。因为通过泊松分布的证明过程，可以把组合数、概率乘方变成用指数表示。（这个图可见fgo抽卡是多么难出货，要理性氪金啊！）
• 伽马分布：$X \sim \Gamma(\alpha,\beta)$ 说的是事件平均概率$\frac{1}{\beta}$ 的时候等到第 $\alpha$个事件发生的时间X符合伽马分布 以上就是它们之间的关系。提这个是因为指数分布、卡方分布都是伽马分布的特例。指数分布只能表示发生事件，不能算等到发生了第k个事件的概率。后者可以用二项分布计算（也是组合数乘以概率），之后转化成用伽马分布表示。

显著性检验

Z检验

有一个来自正态分布总体的样本$X_i\ldots$，已知（指定）总体的$\sigma^2$，想知道总体均值$\mu$和给的$\mu_0$有没有显著差异。于是零假设是$\mu=\mu_0$，用统计量$Z=\frac{\mu-\mu_0}{\sigma\sqrt n}$在正态分布里找拒绝域。

t检验

单样本的

有一个来自正态分布总体的样本$X_i\ldots$，不知道总体的$\sigma^2$和$\mu_0$，想知道总体均值$\mu$和给的$\mu_0$有没有显著差异。于是零假设是$\mu=\mu_0$，用样本标准差$S^2$代替$\sigma^2$，用统计量$t=\frac{\mu-\mu_0}{S\sqrt n} \sim t(n-1)$在学生分布（t分布）里找拒绝域。 因为是用样本估计了总体的标准差，所以不能用正态分布了。学生分布当时被发明出来就是为了解决这个问题的，它的概率密度函数$f(t)$里面有一个自由度（$n-1$）的参数。

双样本的、配对的等等

统计量算的方式有差别。 Minitab帮助 维基

F检验

又叫联合假设检验、方差齐性检验。t检验要求两个总体方差相等的时候就要先检验方差齐性。 有两个正态样本，想检验两个总体的方差是否有显著差异。构造统计量$F=\frac{U_1/d_1}{U_2/d_2}$，$U_1$和$U_2$呈卡方分布，它们的自由度分别是$d_1$和$d_2$。

卡方分布

符合标准正态分布的随机变量的平方和服从自由度为 k 的卡方分布。比如有一个来自正态分布总体的样本$X_i\ldots$，不知道总体的$\sigma^2$和$\mu_0$，想知道总体方差$\sigma^2$和给的$\sigma^2_0$有没有显著差异。样本的标准差$S$是总体标准差的无偏估计，再除以$\sigma_0^2$就正好凑出来一个标准正态分布。统计量$\frac{(n-1)S^2}{\sigma_0^2}\sim \chi(n-1)$，在卡方分布函数里找拒绝域。

线性回归中的显著性检验

检验一个回归系数

用t检验，零假设为回归系数$\beta$是0，。从最小二乘求出回归系数的方法可知，回归系数的标准差$S_\beta=\frac{\sigma}{\sqrt{\Sigma(x_i-\bar x)^2}}$，但总体$y$的标准差$\sigma$不知道，所以用样本的$S_y$代替。计算统计量$t=\frac{\beta}{S_\beta} \sim t(n-2)$。

检验所有的回归系数

用f检验，零假设为所有的回归系数都是0。为了验证这一点，使用了三个平方和（间接表现出零假设的影响）：

• SSM/SSR (Sum of Squares for Model/Regression)
• SSE (Sum of Squares for Error)
• SST (Sum of Squares Total) 关系：SST（样本值和样本平均值之差的平方和）=SSM（预测值和平均值之差的平方和）+ SSE（预测值和样本值之差的平方和）。顺便一提，判定系数$r^2=\frac{SSM}{SST}$。 把SSM和SSE都除以$\sigma^2$就能构造两个符合卡方分布的变量，相除之后消去不知道的方差。 最终得到统计量$F=\frac{SSM/p}{SSE/n-p-1} \sim F(p,n-p-1)$，在F分布函数里找拒绝域。

ANOVA

主要的零假设就是几个样本的均值相等，即没有显著性差异。为了验证这一点，用的基本就是上面显著性检验的方法。 在检验两组之间的差异的时候，就可以用t检验；而在多组的时候，虽然可以两两做t检验，但是不能替代原有的假设，所以用F检验。F检验时也是用组间之差的平方和比上组内之差的平方和。跟回归系数检验里面的F检验一个道理。 总之就是没有特别的方法，就是上面方法的综合运用。